
✳️ 모집단과 표본
⭐ 모집단 : 전체 집단
⭐ 표본 : 모집단에서 추출한 일부

✳️ 표본오차와 신뢰구간
⭐ 표본오차(Sampling error)
- 표본에서 계산된 통계량과 모집단의 진짜 값 간의 차이
- 표본 크기가 클수록 표본오차는 작아짐
=> 표본이 모집단을 완벽하게 대표하지 못하기 때문에 발생하며, 표본의 크기와 표본 추출 방법에 따라 달라질 수 있음- 표본의 크기
: 표본의 크기가 클수록 표본오차는 줄어듬. 더 많은 데이터를 수집할수록 모집단을 더 잘 대표하게 됨 - 표본 추출 방법
: 무작위 추출 방법을 사용하면 표본오차를 줄일 수 있음. 모든 모집단 요소가 선택될 동등한 기회를 가지게 해야 함
- 표본의 크기
⭐ 신뢰구간(Confidence interval)
- 신뢰구간은 모집단의 특정 파라미터(ex: 평균, 비율)에 대해 추정된 값이 포함될 것으로 기대되는 범위를 나타냄
- 신뢰구간 계산 방법
- 신뢰구간 = 표본평균 ± z × 표준오차
- 여기서 z는 선택된 신뢰수준에 해당하는 z-값. ex) 95% 신뢰수준의 z-값은 1.96입니다.
- 일반적으로 95% 신뢰수준을 많이 사용
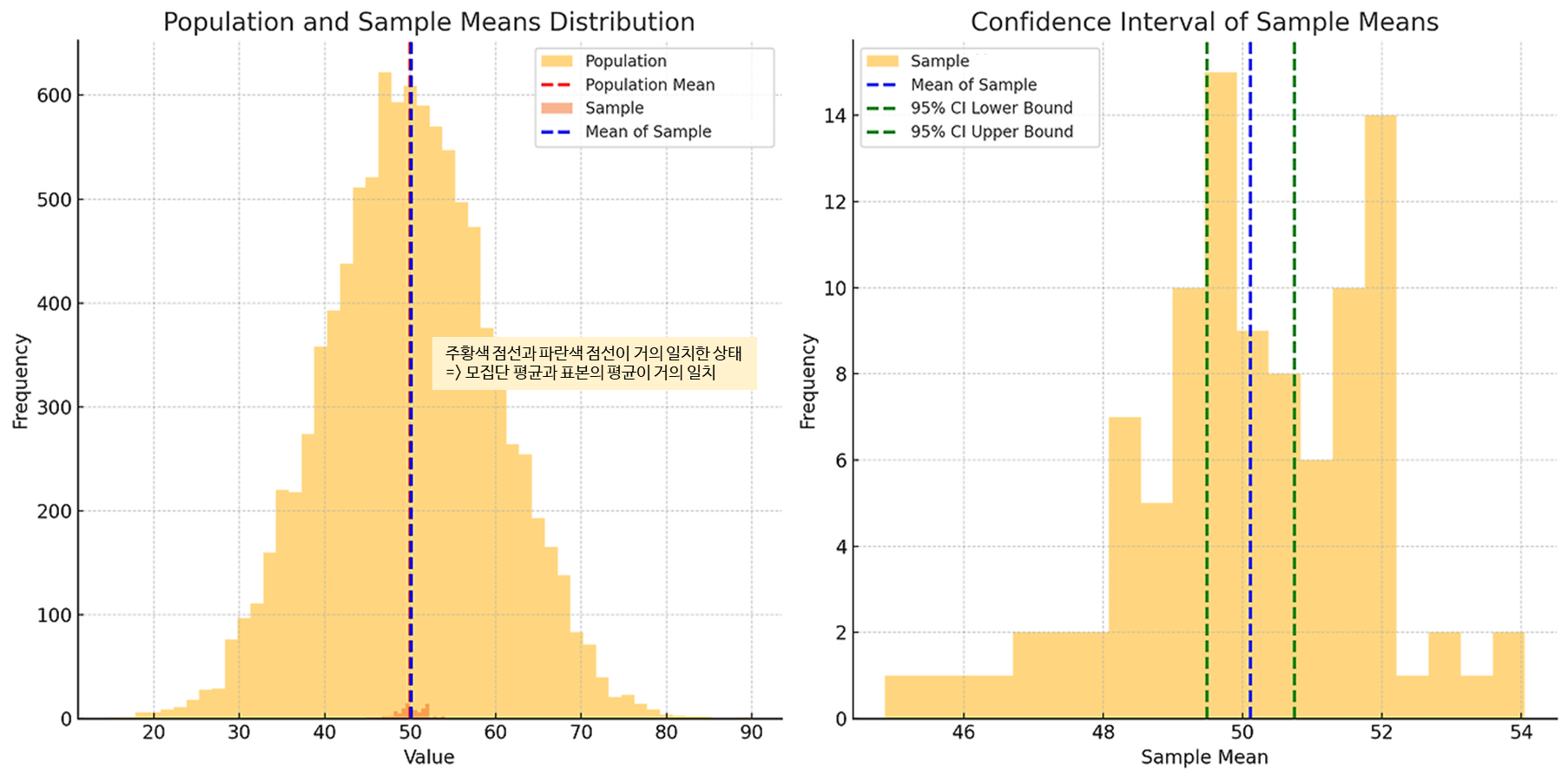
- 모집단과 표본 분포 (왼쪽 그림)
- 붉은색 점선은 모집단의 평균
- 파란색 점선은 표본의 평균
- 모집단의 분포는 넓고, 표본 평균들의 분포는 좁아짐
- 표본 크기가 커질수록 표본 평균이 모집단 평균에 더 가까워지는 경향을 보여줌
- 신뢰구간 시각화 (오른쪽 그림)
- 오른쪽 그림은 표본의 분포와 95% 신뢰구간을 보여줌
- 파란색 점선은 표본의 평균을 나타내고, 녹색 점선은 95% 신뢰구간의 상한과 하한을 나타냄
- 이 신뢰구간은 모집단의 평균을 포함할 것으로 예상되는 범위
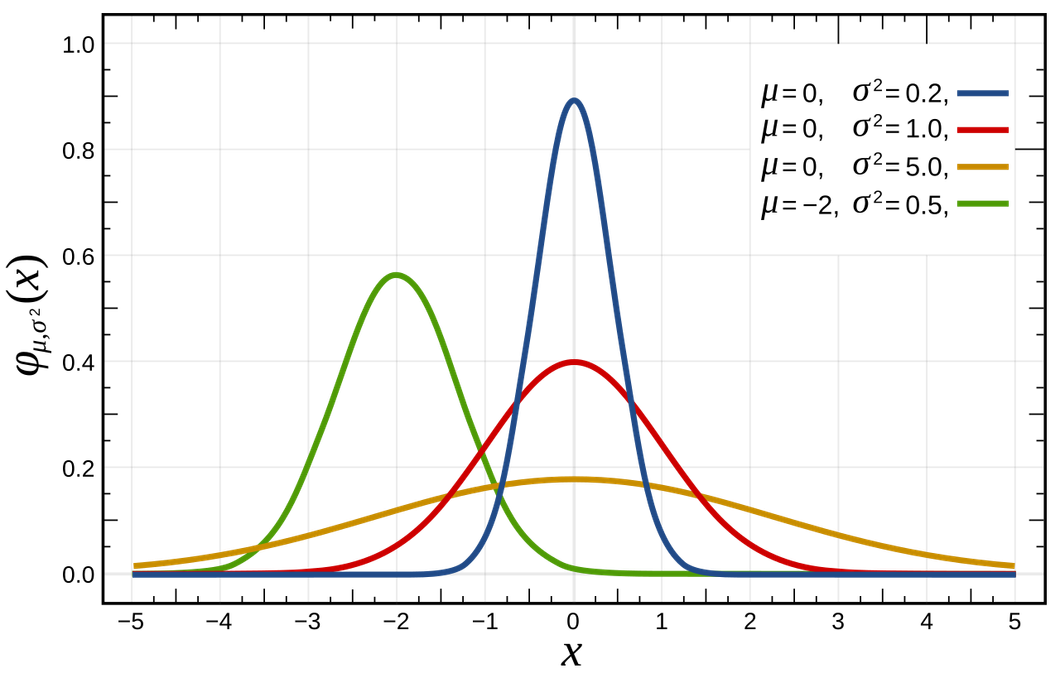
✳️ 정규분포
- 정규분포는 종 모양의 대칭 분포로, 대부분의 데이터가 평균 주위에 몰려 있는 분포
- 평균을 중심으로 좌우 대칭이며, 평균에서 멀어질수록 데이터의 빈도가 감소
- 표준편차는 분포의 퍼짐 정도를 나타냄
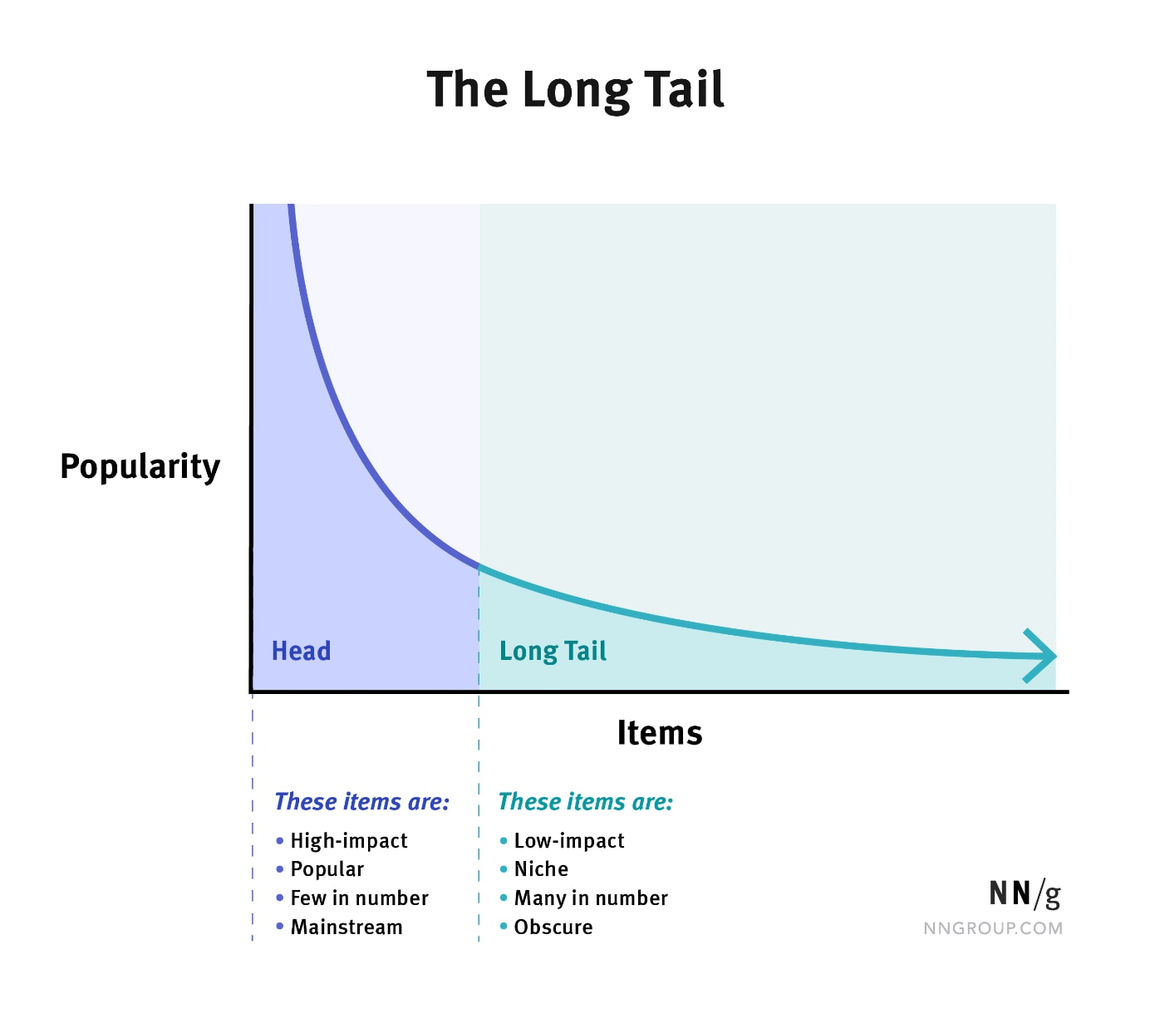
✳️ 긴 꼬리 분포
- 긴 꼬리 분포는 대부분의 데이터가 분포의 한쪽 끝에 몰려 있고, 반대쪽으로 긴 꼬리가 이어지는 형태의 분포
- 이는 정규분포와 달리 대칭적이지 않고 비대칭적
- 특정한 하나의 분포를 의미하지 않으며 여러 종류의 분포(예: 파레토 분포, 지프의 법칙, 멱함수)를 포함할 수 있음
✳️ 스튜던트 t 분포
- t분포는 모집단의 표준편차를 알 수 없고 표본의 크기가 작은 경우(일반적으로 30미만)에 사용되는 분포
- 정규분포와 유사하지만, 표본의 크기가 작을수록 꼬리가 두꺼워지는 특징이 있음
- 자유도(표본의 크기와 관련이 있는 )가 커지면 정규분포에 가까워짐

✳️ 카이제곱 분포
- 카이제곱분포는 범주형 데이터의 독립성 검정이나 적합도 검정에 사용되는 분포
- 자유도(k값, 표본의 크기와 관련있는 값)에 따라 모양이 달라짐
- 상관관계나 인과관계를 판별하고자 하는 원인의 독립변수가 ‘완벽하게 서로 다른 질적 자료’일 때 활용

✳️ 이항분포
- 이항분포는 연속된 값을 가지지 않고, 특정한 정수 값만을 가질 수 있음.
예를 들어, 동전을 10번 던질 때 앞면이 나오는 횟수는 0, 1, 2, ..., 10과 같은 정수.
따라서 이항분포가 연속적으로 그려지지 않음 - 이런 이항분포처럼 연속된 값을 가지지 않는 분포를 이산형 분포라고 지칭 하기도 함
- 성공/실패와 같은 두 가지 결과를 가지는 실험을 여러 번 반복했을 때 성공 횟수의 분포
- 실험 횟수(n)와 성공 확률(p)로 정의

✳️ 푸아송분포
- 단위 시간 또는 단위 면적 당 발생하는 사건의 수를 모델링할 때 사용하는 분포
- 푸아송 분포는 평균 발생률 λ를 가진 사건이 주어진 시간 또는 공간 내에서 몇 번 발생하는지를 나타냄
- 이항 분포처럼 연속된 값을 가지지 않기 때문에 이 분포도 역시 이산형 분포에 해당
- 평균 발생률 λ가 충분히 크다면 정규분포에 근사
- 평균 발생률이란 주어신 시간이나 공간에서 사건이 몇번 발생했는지?
ex) 한 시간동안 콜센터에 전화오는 건수가 10건이면 λ는 10 - 푸아송 분포는 단위 시간 또는 단위 면적당 희귀하게 발생하는 사건의 수를 모델링하는 데 적합

🪄 요약

'📒 Today I Learn > 📈 Statistics' 카테고리의 다른 글
| [통계학 기초] 유의성 검정 (0) | 2024.08.06 |
|---|---|
| [통계학 기초] 데이터의 분포 실습 (0) | 2024.08.05 |
| [통계학 기초] 다양한 분석 방법 (실습) (0) | 2024.08.02 |
| [통계학 기초] 기술 통계와 추론 통계 (0) | 2024.08.02 |
| [통계] 산포도 (Dispersion) (0) | 2024.07.11 |
