
✳️ 모집단과 표본 실습
import numpy as np
import matplotlib.pyplot as plt
# 모집단 생성 (예: 국가의 모든 성인의 키 데이터)
population = np.random.normal(170, 10, 1000)
# 표본 추출
sample = np.random.choice(population, 100)
plt.hist(population, bins=50, alpha=0.5, label='population', color='g')
plt.hist(sample, bins=50, alpha=0.5, label='sample', color='r')
plt.legend()
plt.title('population and sample distribution')
plt.show()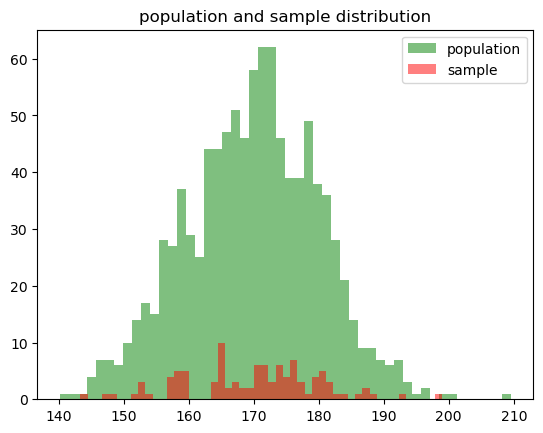
🤔 numpy.random
NumPy 라이브러리의 일부로 다양한 확률 분포에 따라 난수를 생성하는 기능 제공
⭐ np.random.normal
- 함수는 정규분포(가우시안 분포)를 따르는 난수를 생성
numpy.random.normal(loc=0.0, scale=1.0, size=None)- loc (float) : 정규분포의 평균 (기본값: 0.0)
- scale (float) : 정규분포의 표준편차 (기본값: 1.0)
- size (int or tuple of ints) : 출력 배열의 크기 (기본값: None, 즉 스칼라 값 반환)
⭐ np.random.choice
- 주어진 배열에서 임의로 샘플링하여 요소를 선택
- 이는 지정된 배열에서 무작위로 선택된 요소를 반환하는 기능을 제공
numpy.random.choice(a, size=None, replace=True, p=None)- a (1-D array-like or int) : 샘플링할 원본 배열. 정수인 경우 np.arange(a)와 동일하게 간주
- size (int 또는 tuple of ints) : 출력 배열의 크기 (기본값: None, 즉 단일 값 반환)
- replace (boolean) : 복원 추출 여부를 나타냄. True면 동일한 요소가 여러 번 선택될 수 있음 (기본값: True)
- p (1-D array-like, optional) : 각 요소가 선택될 확률. 배열의 합은 1이어야 함
✳️ 표본오차와 신뢰구간 실습
import scipy.stats as stats
# 표본 평균과 표본 표준편차 계산
sample_mean = np.mean(sample)
sample_std = np.std(sample)
# 95% 신뢰구간 계산
conf_interval = stats.t.interval(0.95, len(sample)-1, loc=sample_mean, scale=sample_std/np.sqrt(len(sample)))
print(f"표본 평균: {sample_mean}")
print(f"95% 신뢰구간: {conf_interval}")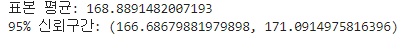
🤔 stats.t.interval
scipy.stats는 SciPy 라이브러리의 일부로, 통계 분석을 위한 다양한 함수와 클래스들을 제공하는 모듈
scipy.stats.t.interval 함수는 주어진 신뢰 수준에서 t-분포를 사용하여 신뢰 구간을 계산하는 데 사용
scipy.stats.t.interval(alpha, df, loc=0, scale=1)- alpha
신뢰 수준(confidence level)을 의미
예를 들어, 95% 신뢰 구간을 원하면 alpha를 0.95로 설정 - df
자유도(degrees of freedom)를 나타냄
일반적으로 표본 크기에서 1을 뺀 값으로 설정 (df = n - 1) - loc
위치(parameter of location)로, 일반적으로 표본 평균을 설정 - scale
스케일(parameter of scale)로, 일반적으로 표본 표준 오차(standard error)를 설정.
표본 표준 오차는 표본 표준편차를 표본 크기의 제곱근으로 나눈 값 (scale = sample_std / sqrt(n))
✳️ 정규분포 실습
# 정규분포 생성
normal_dist = np.random.normal(170, 10, 1000)
# 히스토그램으로 시각화
plt.hist(normal_dist, bins=30, density=True, alpha=0.6, color='g')
# 정규분포 곡선 추가
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = stats.norm.pdf(x, 170, 10)
plt.plot(x, p, 'k', linewidth=2)
plt.title('normal distribution histogram')
plt.show()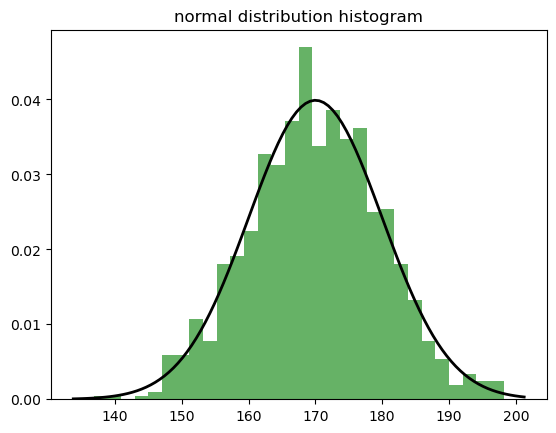
✳️ 긴 꼬리 분포 실습
# 긴 꼬리 분포 생성 (예: 소득 데이터)
long_tail = np.random.exponential(1, 1000)
# 히스토그램으로 시각화
plt.hist(long_tail, bins=30, density=True, alpha=0.6, color='g')
plt.title('long tail distribution histogram')
plt.show()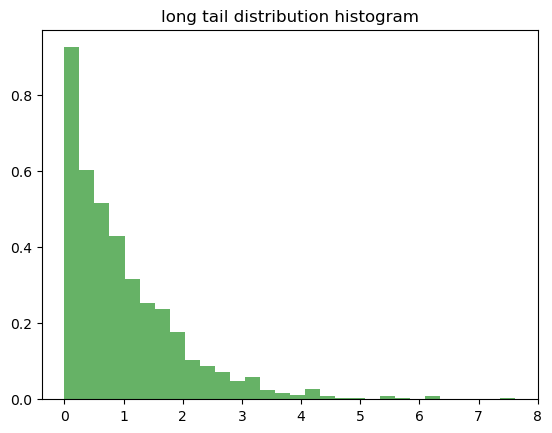
✳️ student t 분포 실습
# 스튜던트 t 분포 생성
t_dist = np.random.standard_t(df=10, size=1000)
# 히스토그램으로 시각화
plt.hist(t_dist, bins=30, density=True, alpha=0.6, color='r')
# 스튜던트 t 분포 곡선 추가
x = np.linspace(-4, 4, 100)
p = stats.t.pdf(x, df=10)
plt.plot(x, p, 'k', linewidth=2)
plt.title('student t distribution histogram')
plt.show()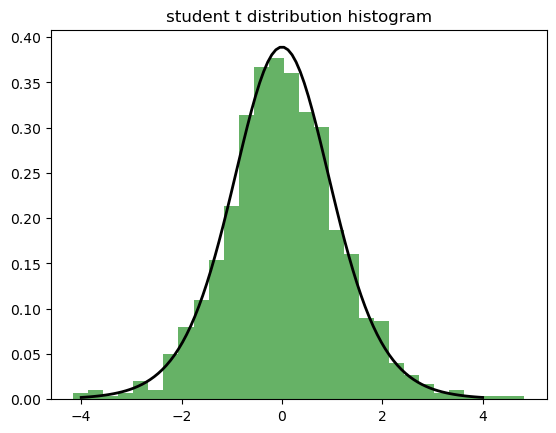
✳️ 카이제곱분포 실습
# 카이제곱분포 생성
chi2_dist = np.random.chisquare(df=2, size=1000)
# 히스토그램으로 시각화
plt.hist(chi2_dist, bins=30, density=True, alpha=0.6, color='m')
# 카이제곱분포 곡선 추가
x = np.linspace(0, 10, 100)
p = stats.chi2.pdf(x, df=2)
plt.plot(x, p, 'k', linewidth=2)
plt.title('카이제곱 분포 히스토그램')
plt.show()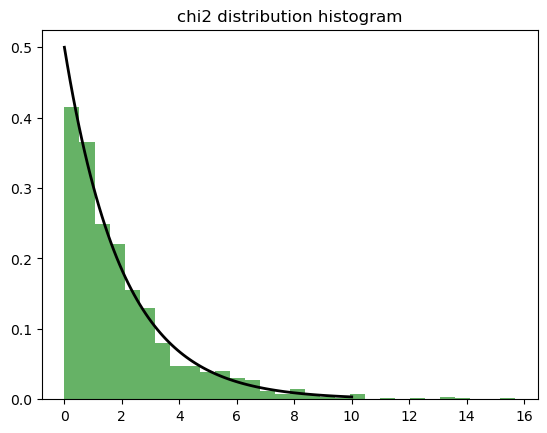
✳️ 이항분포 실습
# 이항분포 생성 (예: 동전 던지기 10번 중 앞면이 나오는 횟수)
binom_dist = np.random.binomial(n=10, p=0.5, size=1000)
# 히스토그램으로 시각화
plt.hist(binom_dist, bins=10, density=True, alpha=0.6, color='g')
plt.title('binomial distribultion histogram')
plt.show()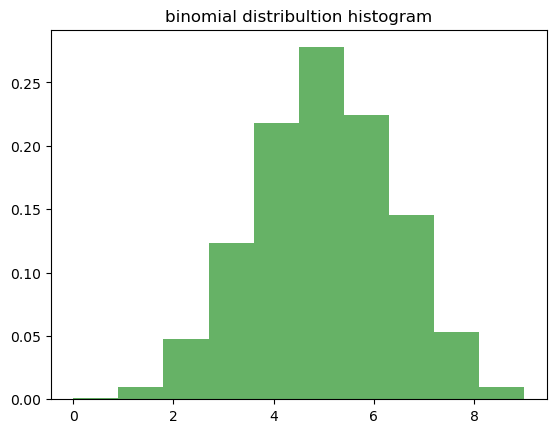
✳️ 푸아송분포 실습
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# 푸아송 분포 파라미터 설정
lambda_value = 4 # 평균 발생률
x = np.arange(0, 15) # 사건 발생 횟수 범위
# 푸아송 분포 확률 질량 함수 계산
poisson_pmf = poisson.pmf(x, lambda_value)
# 그래프 그리기
plt.figure(figsize=(10, 6))
plt.bar(x, poisson_pmf, alpha=0.6, color='g', label=f'Poisson PMF (lambda={lambda_value})')
plt.xlabel('Number of Events')
plt.ylabel('Probability')
plt.title('Poisson Distribution')
plt.legend()
plt.grid(True)
plt.show()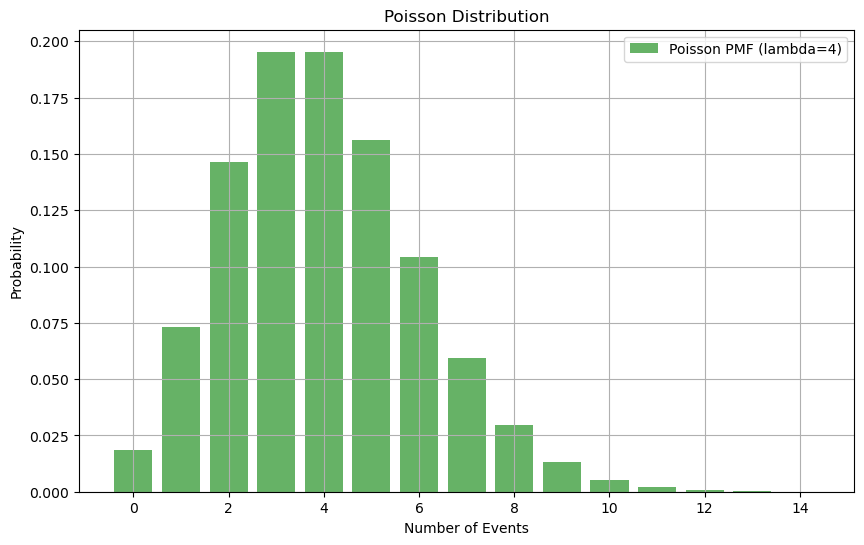
'📒 Today I Learn > 📈 Statistics' 카테고리의 다른 글
| [통계학 기초] 유의성 검정 실습 (0) | 2024.08.06 |
|---|---|
| [통계학 기초] 유의성 검정 (0) | 2024.08.06 |
| [통계학 기초] 데이터의 분포 (0) | 2024.08.05 |
| [통계학 기초] 다양한 분석 방법 (실습) (0) | 2024.08.02 |
| [통계학 기초] 기술 통계와 추론 통계 (0) | 2024.08.02 |

✳️ 모집단과 표본 실습
import numpy as np
import matplotlib.pyplot as plt
# 모집단 생성 (예: 국가의 모든 성인의 키 데이터)
population = np.random.normal(170, 10, 1000)
# 표본 추출
sample = np.random.choice(population, 100)
plt.hist(population, bins=50, alpha=0.5, label='population', color='g')
plt.hist(sample, bins=50, alpha=0.5, label='sample', color='r')
plt.legend()
plt.title('population and sample distribution')
plt.show()
🤔 numpy.random
NumPy 라이브러리의 일부로 다양한 확률 분포에 따라 난수를 생성하는 기능 제공
⭐ np.random.normal
- 함수는 정규분포(가우시안 분포)를 따르는 난수를 생성
numpy.random.normal(loc=0.0, scale=1.0, size=None)- loc (float) : 정규분포의 평균 (기본값: 0.0)
- scale (float) : 정규분포의 표준편차 (기본값: 1.0)
- size (int or tuple of ints) : 출력 배열의 크기 (기본값: None, 즉 스칼라 값 반환)
⭐ np.random.choice
- 주어진 배열에서 임의로 샘플링하여 요소를 선택
- 이는 지정된 배열에서 무작위로 선택된 요소를 반환하는 기능을 제공
numpy.random.choice(a, size=None, replace=True, p=None)- a (1-D array-like or int) : 샘플링할 원본 배열. 정수인 경우 np.arange(a)와 동일하게 간주
- size (int 또는 tuple of ints) : 출력 배열의 크기 (기본값: None, 즉 단일 값 반환)
- replace (boolean) : 복원 추출 여부를 나타냄. True면 동일한 요소가 여러 번 선택될 수 있음 (기본값: True)
- p (1-D array-like, optional) : 각 요소가 선택될 확률. 배열의 합은 1이어야 함
✳️ 표본오차와 신뢰구간 실습
import scipy.stats as stats
# 표본 평균과 표본 표준편차 계산
sample_mean = np.mean(sample)
sample_std = np.std(sample)
# 95% 신뢰구간 계산
conf_interval = stats.t.interval(0.95, len(sample)-1, loc=sample_mean, scale=sample_std/np.sqrt(len(sample)))
print(f"표본 평균: {sample_mean}")
print(f"95% 신뢰구간: {conf_interval}")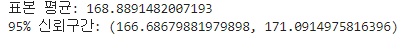
🤔 stats.t.interval
scipy.stats는 SciPy 라이브러리의 일부로, 통계 분석을 위한 다양한 함수와 클래스들을 제공하는 모듈
scipy.stats.t.interval 함수는 주어진 신뢰 수준에서 t-분포를 사용하여 신뢰 구간을 계산하는 데 사용
scipy.stats.t.interval(alpha, df, loc=0, scale=1)- alpha
신뢰 수준(confidence level)을 의미
예를 들어, 95% 신뢰 구간을 원하면 alpha를 0.95로 설정 - df
자유도(degrees of freedom)를 나타냄
일반적으로 표본 크기에서 1을 뺀 값으로 설정 (df = n - 1) - loc
위치(parameter of location)로, 일반적으로 표본 평균을 설정 - scale
스케일(parameter of scale)로, 일반적으로 표본 표준 오차(standard error)를 설정.
표본 표준 오차는 표본 표준편차를 표본 크기의 제곱근으로 나눈 값 (scale = sample_std / sqrt(n))
✳️ 정규분포 실습
# 정규분포 생성
normal_dist = np.random.normal(170, 10, 1000)
# 히스토그램으로 시각화
plt.hist(normal_dist, bins=30, density=True, alpha=0.6, color='g')
# 정규분포 곡선 추가
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = stats.norm.pdf(x, 170, 10)
plt.plot(x, p, 'k', linewidth=2)
plt.title('normal distribution histogram')
plt.show()
✳️ 긴 꼬리 분포 실습
# 긴 꼬리 분포 생성 (예: 소득 데이터)
long_tail = np.random.exponential(1, 1000)
# 히스토그램으로 시각화
plt.hist(long_tail, bins=30, density=True, alpha=0.6, color='g')
plt.title('long tail distribution histogram')
plt.show()
✳️ student t 분포 실습
# 스튜던트 t 분포 생성
t_dist = np.random.standard_t(df=10, size=1000)
# 히스토그램으로 시각화
plt.hist(t_dist, bins=30, density=True, alpha=0.6, color='r')
# 스튜던트 t 분포 곡선 추가
x = np.linspace(-4, 4, 100)
p = stats.t.pdf(x, df=10)
plt.plot(x, p, 'k', linewidth=2)
plt.title('student t distribution histogram')
plt.show()
✳️ 카이제곱분포 실습
# 카이제곱분포 생성
chi2_dist = np.random.chisquare(df=2, size=1000)
# 히스토그램으로 시각화
plt.hist(chi2_dist, bins=30, density=True, alpha=0.6, color='m')
# 카이제곱분포 곡선 추가
x = np.linspace(0, 10, 100)
p = stats.chi2.pdf(x, df=2)
plt.plot(x, p, 'k', linewidth=2)
plt.title('카이제곱 분포 히스토그램')
plt.show()
✳️ 이항분포 실습
# 이항분포 생성 (예: 동전 던지기 10번 중 앞면이 나오는 횟수)
binom_dist = np.random.binomial(n=10, p=0.5, size=1000)
# 히스토그램으로 시각화
plt.hist(binom_dist, bins=10, density=True, alpha=0.6, color='g')
plt.title('binomial distribultion histogram')
plt.show()
✳️ 푸아송분포 실습
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# 푸아송 분포 파라미터 설정
lambda_value = 4 # 평균 발생률
x = np.arange(0, 15) # 사건 발생 횟수 범위
# 푸아송 분포 확률 질량 함수 계산
poisson_pmf = poisson.pmf(x, lambda_value)
# 그래프 그리기
plt.figure(figsize=(10, 6))
plt.bar(x, poisson_pmf, alpha=0.6, color='g', label=f'Poisson PMF (lambda={lambda_value})')
plt.xlabel('Number of Events')
plt.ylabel('Probability')
plt.title('Poisson Distribution')
plt.legend()
plt.grid(True)
plt.show()
'📒 Today I Learn > 📈 Statistics' 카테고리의 다른 글
| [통계학 기초] 유의성 검정 실습 (0) | 2024.08.06 |
|---|---|
| [통계학 기초] 유의성 검정 (0) | 2024.08.06 |
| [통계학 기초] 데이터의 분포 (0) | 2024.08.05 |
| [통계학 기초] 다양한 분석 방법 (실습) (0) | 2024.08.02 |
| [통계학 기초] 기술 통계와 추론 통계 (0) | 2024.08.02 |
