
✳️ A / B 검정 실습
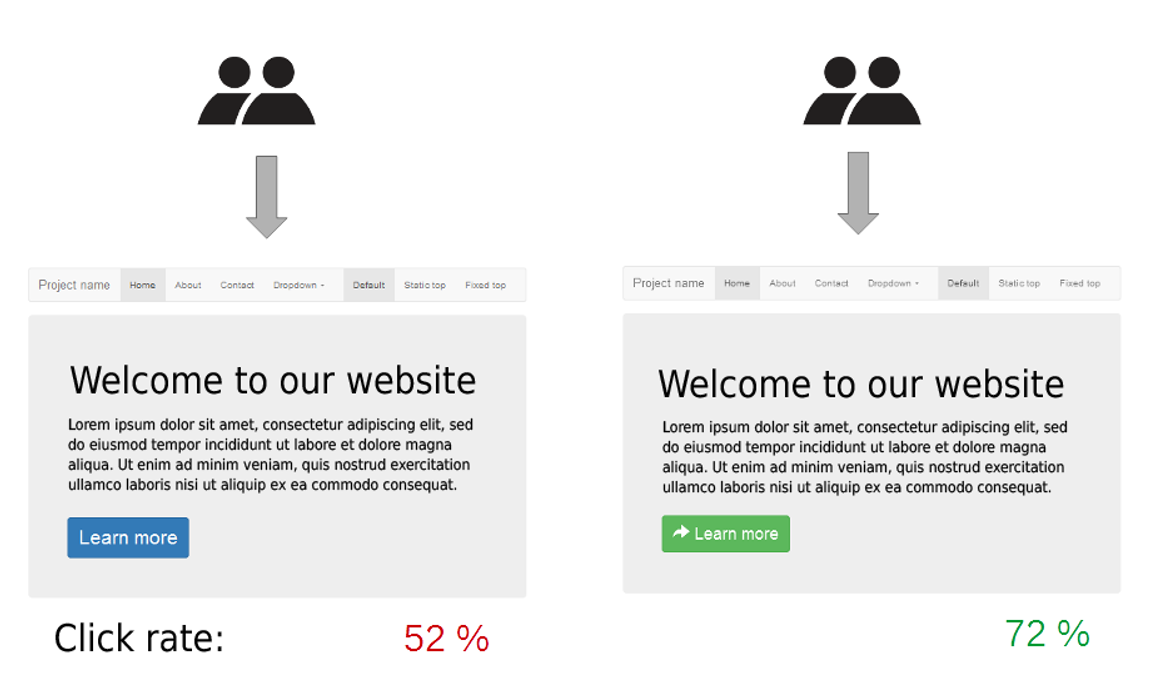
A디자인과 B디자인의 전환률 -> B가 더 크다
과연 진짜로 차이가 난 것일까? A/B검정을 통해 알아보자!
import numpy as np
import scipy.stats as stats
# 가정된 전환율 데이터
group_a = np.random.binomial(1, 0.30, 100) # 30% 전환율
group_b = np.random.binomial(1, 0.45, 100) # 45% 전환율
# t-test를 이용한 비교
t_stat, p_val = stats.ttest_ind(group_a, group_b)
print(f"T-Statistic: {t_stat}, P-value: {p_val}")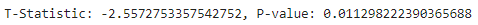
t-test를 통해서 검정을 해보면 p-value가 0.05보다 낮게 나온 것을 볼 수 있고, 이를 통해 통계적으로 의미가 있어 진짜로 전환율의 차이가 있었다고 해석해볼 수 있다.
🤔 stats.ttest_ind
▶ scipy.stats.test_ind 함수는 독립표본 t-검정(Independent Samples t-test)을 수행하여 두 개의 독립된 집단 간 평균의 차이가 유의미한지 평가
▶ 이 함수는 두 집단의 데이터 배열을 입력으로 받아서 t-통계량과 p-값을 반환
✓ t-통계량 (statistic)
✓ p-값 (pvalue)
- t-검정 통계량. 두 집단 간 평균 차이의 크기와 방향을 나타냄
- p-값은 귀무 가설이 참일 때, 현재 데이터보다 극단적인 결과가 나올 확률
- 이 값이 유의수준(α) 보다 작으면 귀무 가설을 기각하고 이 값이 유의수준(α) 보다 크면 귀무 가설을 채택
✳️ 가설검정 실습
기존 A 약물과 새로 B 약물의 효과를 표본에 적용하여 실험을 했을 때,
모집단에서도 새로운 B 약물의 효능이 있는지 없는지를 결론 내리려고 한다.
가설 검정을 통해서 p-value 값을 보고 판단을 해보자!
# 기존 약물(A)와 새로운 약물(B) 효과 데이터 생성
A = np.random.normal(50, 10, 100)
B = np.random.normal(55, 10, 100)
# 평균 효과 계산
mean_A = np.mean(A)
mean_B = np.mean(B)
# t-검정 수행
t_stat, p_value = stats.ttest_ind(A, B)
print(f"A 평균 효과: {mean_A}")
print(f"B 평균 효과: {mean_B}")
print(f"t-검정 통계량: {t_stat}")
print(f"p-값: {p_value}")
# t-검정의 p-값 확인 (위 예시에서 계산된 p-값 사용)
print(f"p-값: {p_value}")
if p_value < 0.05:
print("귀무가설을 기각합니다. 통계적으로 유의미한 차이가 있습니다.")
else:
print("귀무가설을 기각하지 않습니다. 통계적으로 유의미한 차이가 없습니다.")
기존 약물 A와 새로운 약물 B의 효과에 대한 평균을 서로 비교하여 t-test를 진행 했을 때, p값이 0.05보다 낮게 나오는 것으로 확인되었다. 따라서 유의미한 차이가 있기 때문에 B 약물의 효과가 있다 라고 판단을 할 수 있다.
✳️ t 검정 실습

어떤 집단의 점수 데이터를 가지고 평균을 비교하여 p-value를 통해
두 집단이 얼마나 연관이 되어있는지 확인하고자 한다!
# 학생 점수 데이터
scores_method1 = np.random.normal(70, 10, 30)
scores_method2 = np.random.normal(75, 10, 30)
# 독립표본 t검정
t_stat, p_val = stats.ttest_ind(scores_method1, scores_method2)
print(f"T-Statistic: {t_stat}, P-value: {p_val}")
p-value를 확인하면 0.05보다 낮으므로 두 집단은 서로 다른 집단이라고 결론을 내릴 수 있다.
✳️ 다중검정 실습
어떠한 세 집단을 t-test를 통해 p-value 값으로 서로 간의 유의미한 차이가 있는지 확인해보려고 한다.
import numpy as np
import scipy.stats as stats
# 세 그룹의 데이터 생성
np.random.seed(42)
group_A = np.random.normal(10, 2, 30)
group_B = np.random.normal(12, 2, 30)
group_C = np.random.normal(11, 2, 30)
# 세 그룹 간 평균 차이에 대한 t검정 수행
p_values = []
p_values.append(stats.ttest_ind(group_A, group_B).pvalue)
p_values.append(stats.ttest_ind(group_A, group_C).pvalue)
p_values.append(stats.ttest_ind(group_B, group_C).pvalue)
# 본페로니 보정 적용
alpha = 0.05
adjusted_alpha = alpha / len(p_values)
# 결과 출력
print(f"본페로니 보정된 유의 수준: {adjusted_alpha:.4f}")
for i, p in enumerate(p_values):
if p < adjusted_alpha:
print(f"검정 {i+1}: 유의미한 차이 발견 (p = {p:.4f})")
else:
print(f"검정 {i+1}: 유의미한 차이 없음 (p = {p:.4f})")
보정을 적용하기 위해 유의수준을 낮추려고 한다. 그래서 본래의 유의 수준이었던 0.05를 p-value값의 개수로 나누어준다.(0.05 / 3)
유의수준이 훨씬 작아지게 되고 기준을 엄격하게 만들어줬다. 그러나 이 유의수준도 너무 엄격하게 해버리면 제 2종 오류가 늘어날 수 있기 때문에 적절히 이용해야 한다.
그래서 group A와 group B는 서로 비교했을 때 유의미한 차이가 있고,
group B와 group C도 유의미한 차이가 있다.
group A와 group B는 유의미한 차이가 없다고 해석할 수 있다.
✳️ 카이제곱 실습
적합도 검정과 독립성 검정의 예시, 독립성 검정의 세부 예시로 실습해보자!
# 적합도 검정
observed = [20, 30, 25, 25]
expected = [25, 25, 25, 25]
chi2_stat, p_value = stats.chisquare(observed, f_exp=expected)
print(f"적합도 검정 카이제곱 통계량: {chi2_stat}, p-값: {p_value}")
# 독립성 검정
observed = np.array([[10, 10, 20], [20, 20, 40]])
chi2_stat, p_value, dof, expected = stats.chi2_contingency(observed)
print(f"독립성 검정 카이제곱 통계량: {chi2_stat}, p-값: {p_value}")
# 나이와 흡연 여부 독립성 검정
observed = np.array([[30, 10], [20, 40]])
chi2_stat, p_value, dof, expected = stats.chi2_contingency(observed)
print(f"독립성 검정 카이제곱 통계량: {chi2_stat}, p-값: {p_value}")
적합도 검정 : p값이 0.05보다 높다! -> 관측한 결과 값과 본래에 나와야 했던 모집단의 결과값이 차이가 없다!
독립성 검정 : p값이 0.05보다 높다! -> 두 변수가 서로 연관이 없다고 판단, 독립성이 있다!
나이와 흡연 여부 독립성 검정 : p값이 0.05보다 매우 작다! -> 나이와 흡연여부는 독립성이 없고 서로가 연관되어 있다고 판단!
🤔 stats.chisquare
▶ scipy.stats.chisquare 함수는 카이제곱 적합도 검정을 수행하여 관찰된 빈도 분포가 기대된 빈도 분포와 일치하는지 평가. 이 검정은 주로 단일 표본에 대해 관찰된 빈도가 특정 이론적 분포(예: 균등 분포)와 일치하는지 확인하는 데 사용
▶ 반환 값
- chi2 : 카이제곱 통계량
- p : p-값. 관찰된 데이터가 귀무 가설 하에서 발생할 확률
🤔 stats.chi2_contingency
▶ scipy.stats.chi2_contingency 함수는 카이제곱 검정을 수행하여 두 개 이상의 범주형 변수 간의 독립성을 검정
▶ 이 함수는 관측 빈도를 담고 있는 교차표(contingency table)를 입력으로 받아 카이제곱 통계량, p-값, 자유도, 그리고 기대 빈도(expected frequencies)를 반환
▶ 반환 값
- chi2 : 카이제곱 통계량
- p : p-값. 관측된 데이터가 귀무 가설 하에서 발생할 확률
- dof : 자유도. (행의 수 - 1) * (열의 수 - 1)로 계산
- expected : 기대 빈도. 행 합계와 열 합계를 사용하여 계산된 이론적 빈도
'📒 Today I Learn > 📈 Statistics' 카테고리의 다른 글
| [통계학 기초] 회귀 실습 (0) | 2024.08.07 |
|---|---|
| [통계학 기초] 회귀(Regression) (0) | 2024.08.07 |
| [통계학 기초] 유의성 검정 (0) | 2024.08.06 |
| [통계학 기초] 데이터의 분포 실습 (0) | 2024.08.05 |
| [통계학 기초] 데이터의 분포 (0) | 2024.08.05 |
